狂気を感じる動画として一部で話題になった『フカシギの数え方』
僕も数えてみます!
数え上げ問題なので、まずは定石通りに、問題の状態を数値で表現してみて、それぞれの状態から何通りあるかと考える方針でいきます。
この状態を表現するのに、どのような情報が必要でしょうか。
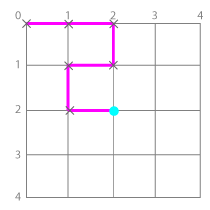
以下の情報があれば、この状態からゴールまでの通り方の数は一意に決まりそうです。
- 現在地: (2,2)
- もう通れない点: (0,0), (1,0), (2,0), (2,1), (1,1), (1,2)
ここからの行き先ですが、左と上はもう通っている点なので行けません。
残りは2通りです。
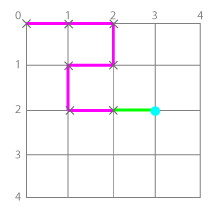
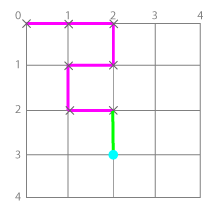
それぞれ、同じように「現在地」と「もう通れない点」から状態を表現できます。
また、この状態だとどうなるでしょう。
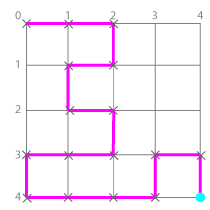
すでにゴールに到達してます。
この状態からゴールまでの通り方の数はもちろん1通りです。
以上から、各状態からのゴールまでの通り方は再帰的に求められます。
- 現在地がゴールなら、1通り
- そうでなければ、上下左右それぞれに(進める場合は)進んだ状態からのゴールまでの通り方を足し合わせる。
具体的なコードはたとえばこんな感じです。
コード例では、「もう通れない点」の集合を楽に表すためにビット演算を使っています。
座標(0,1)と(0,3)をそれぞれ2進数で0001, 0100などと表すと、(0,1)と(0,3)の集合を0101として1つの整数値に押し込められます。
[cpp]
#include <iostream>
const int DX[] = {0, 0, -1, 1};
const int DY[] = {-1, 1, 0, 0};
int W, H;
// 座標(x, y)をビットで表す
long long bit(int x, int y) {
return 1LL << (y * W + x);
}
// 現在の座標と通過済みの座標集合から、パターン数を返す
long long dfs(int x, int y, long long visited) {
// 既にゴールにいるなら、そこからのパターンは1通り
if (x == W-1 && y == H-1) return 1;
// 現在地(x, y)を通過済みとしてマークする
visited |= bit(x, y);
long long res = 0;
// 4つの隣接点でまだ通過してない点があれば、そこに進んだ場合の
// パターン数を合計に加える
for (int i = 0; i < 4; i++) {
int next_x = x + DX[i];
int next_y = y + DY[i];
if (next_x >= 0 && next_x < W && next_y >= 0 && next_y < H) {
if (!(visited & bit(next_x, next_y))) {
res += dfs(next_x, next_y, visited);
}
}
}
return res;
}
int main() {
std::cout << “横は何分割? : “;
std::cin >> W; W++;
std::cout << “縦は何分割? : “;
std::cin >> H; H++;
long long ways = dfs(0, 0, 0LL);
std::cout << ways << ” だってよ!” << std::endl;
}
[/cpp]
結果はこんな感じ。6×6に2分半かかったので、7×7は数百時間にはなりそうです。
[bash]
$ clang++ -O3 main.cpp && time ./a.out
横は何分割? : 6
縦は何分割? : 6
575780564 だってよ!
real 2m37.630s
user 2m37.058s
sys 0m0.035s
[/bash]
4分岐で再帰の深さは最大W*Hなので、ざっくり計算量はO(4^(W*H))でしょうか。
最先端アルゴリズムだとちょっぱやらしいので、しばらく考えてみたんですが何も思いつきませんでした!
(それを探して来た人ごめんなさい ><)
